What is a Neural Network?

The most familiar example of a Neural Network is that of a multi-layer perceptron (MLP), covered in plenty of detail at all levels of understanding¹.

The building blocks of such a network involves fully connected (FC) networks between input and output,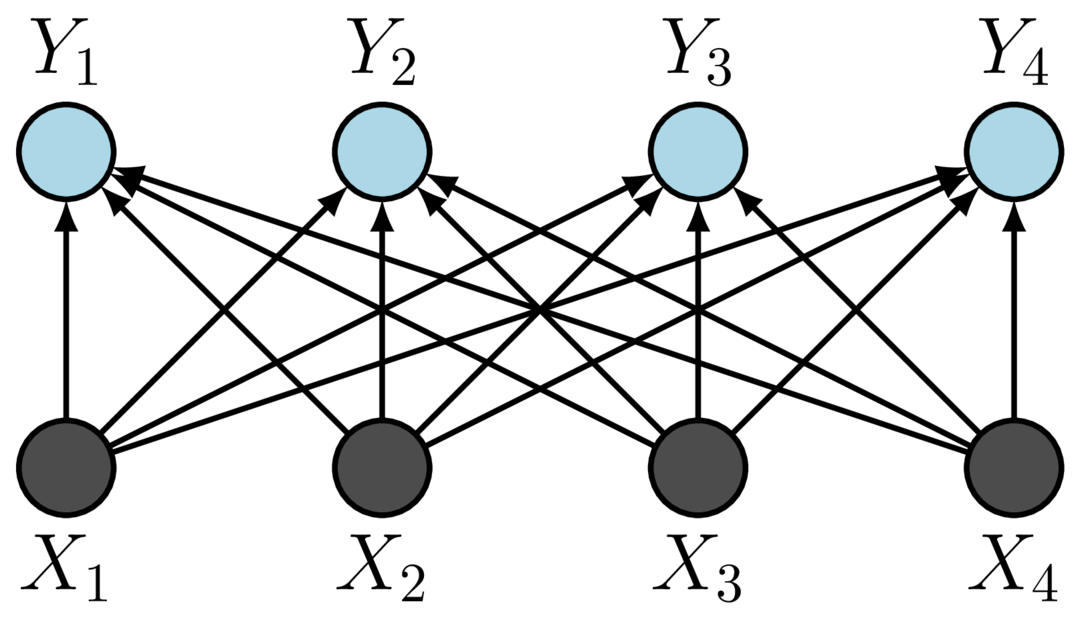

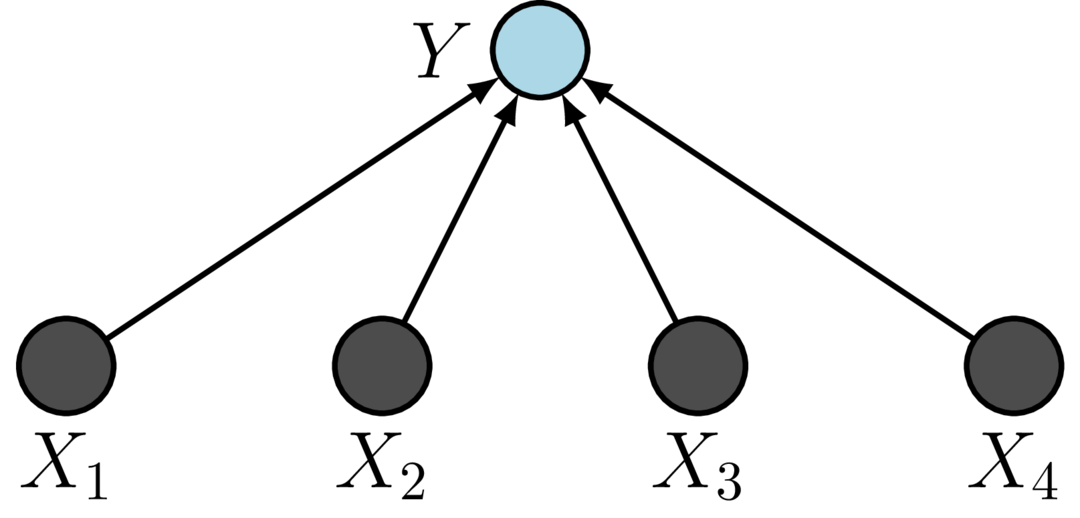
Typically multiple copies of such a transformation (plus appropriate non-linear activation) are applied, before the final layer is connected to an appropriate loss function for the task at hand. A pooling layer is a trivial special case of a FC layer to reduce dimensionality where appropriate,

In effect such a network communicates the connection between all of the inputs via global interactions – all inputs can talk to each other. With additional layers and non linear activations allowing complicated non-linear interaction.

What is a Graph Neural Network?

The paradigm of allowing FC networks and learning all the relevant connections to make from the training data dominated the field of Machine Learning for many years. However for specific tasks it is well motivated to restrict the connections that are possible – for example in image recognition it would be sensible to put emphasis on local interactions when building up an image. The pixels adjacent to each other in an image should have stronger relations to each other than pixels far away. This incidently is the motivation behind Convolutional Neural Networks.

In some ways this thinking is a move back towards more “classical” fitting we would expect in physics, where historically the idea is to fit some well chosen basis functions to a specific task (if I am modelling a process like nuclear decay, I wouldn’t hesitate to choose an exponential function and fit that to my data).

This, in essence, is the insight behind what is sometimes phrased geometric deep learning². A rather nebulously defined concept to define networks that operate on different data structures in a way that preserves some property. Graph Neural Networks are the parent form, from which other geometric deep learning algorithms can be understood as special cases.

Deep Sets

Deep Sets are a simple special case of a Graph Neural Network, and hence are useful for this proposed exploratory analysis of this fast moving area of research. Deep Sets are networks which are invariant under the permutation group, i.e. they are functions that act on sets. That is to say that if my network is a function mapping a set to an output, $$ f({X_1,X_2,X_3,X_4 }) \rightarrow Y$$ Then under permutation of the input set my network remains invariant, $$f({X_2,X_1,X_4,X_3 }) \rightarrow Y$$

To build such a network we have to take a pair of scissors to the previously displayed MLP networks and reduce the FC layer to something that only admits equivariant and invariant operations under the permutation of the inputs,

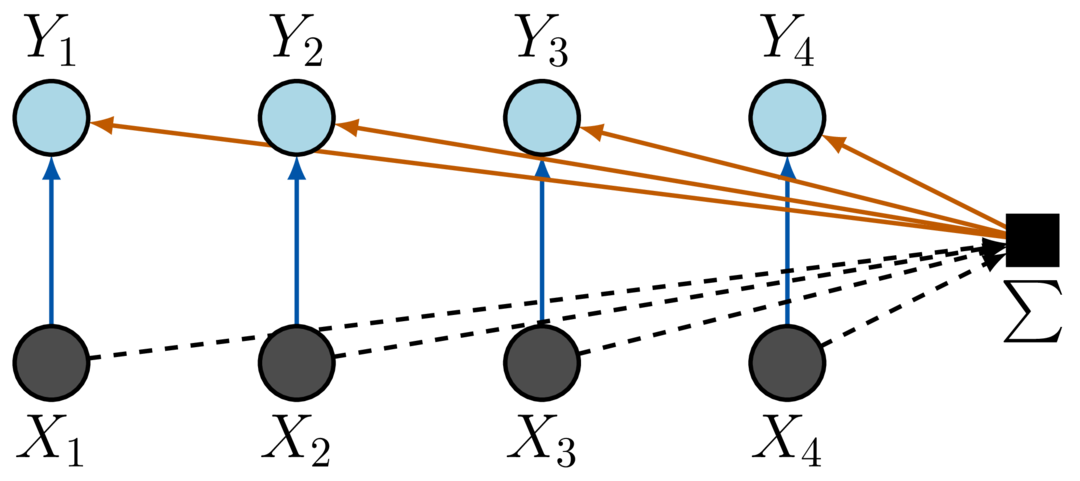
The blue connections are equivariant, one single shared weight is used to connect the inputs to the hidden nodes. If the order of the inputs is swapped then the order of the hidden nodes is equivalently swapped – this is the definition of equivariance. The orange connections are a single shared weight that adds the sum of the input node values back to each hidden node. The summing operation is invariant to the order of nodes. We can also define a pooling operation in the same way which is now reduced to a permutation invariant summation,

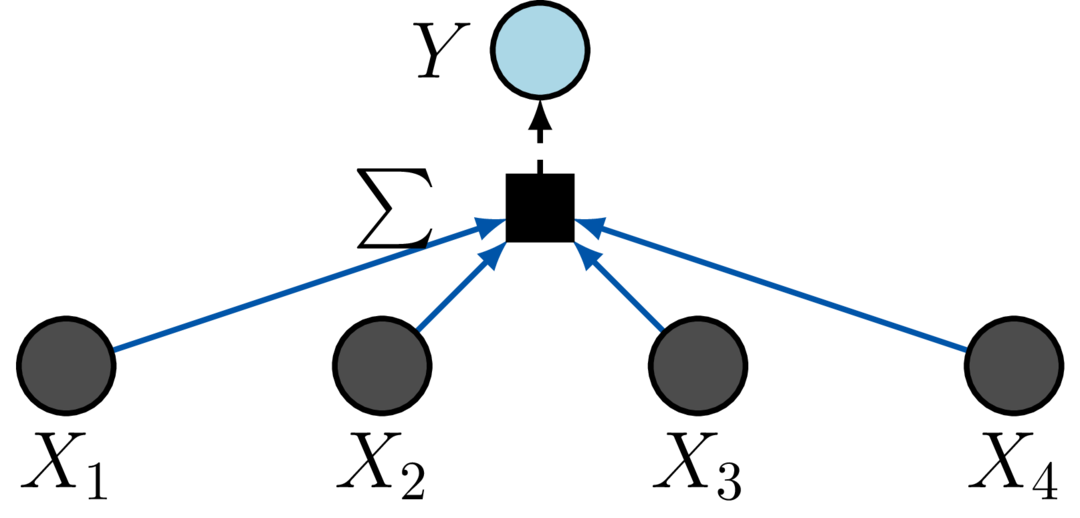
The special operations this network encodes could be learnt by a FC MLP network, however this paradigm both enforces the desired property, and additionally is a much lower dimensional network and hence much easier to work with and understand (vital for explainable AI and well calibrated uncertainties)

The project at hand

There are two reasons to get excited about GNNs from our point of view as physicists.

• There are many tasks in physics that involve some special symmetry preserving operations – we may be able to come up with state of the art approaches to long standing questions in physics.

• We have a great deal of expertise in Bayesian inference in the Cambridge Cosmology group, and these lower dimensional are ideal to approach with principled Bayesian statistics – this could be a vital stepping stone towards the long sought after goal of truly explainable AI