Particle Monte Carlo for Lattice Field Theory
NeurIPS 2025 Workshop Frontiers in Probabilistic Inference
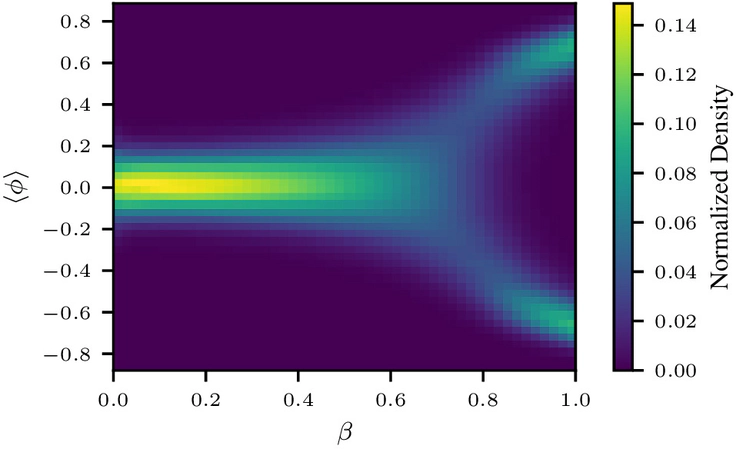 Magnetization density across inverse temperature
Magnetization density across inverse temperaturePresented at NeurIPS 2025 Workshop: Frontiers in Probabilistic Inference | arXiv:2511.15196 | Poster (PDF)
Neural samplers have gained attention for learning flexible trivializing maps in lattice field theory (LFT) problems. However, many of their strengths overlap with existing particle Monte Carlo methods. In much of the ML sampling literature, particle methods are presented as weak baselines. In this work, we revisit a standard field-sampling benchmark to ask: are particle methods really as weak as claimed, and how strong can they be when optimized for GPUs?
Key result: Black-box particle Monte Carlo methods can match or outperform black-box neural samplers, while also estimating the partition function.
Scalar field theory benchmark
We target the two-dimensional scalar \( \phi^4 \) theory, following Hackett et al. (2021), a standard benchmark characterized by strong couplings, multimodal distributions, and high-dimensional state spaces. The action is
$$ \begin{aligned} S(\phi)=\sum_x\left[\frac{1}{2}\sum_{\nu=1}^2(\phi_x-\phi_{x+\hat\nu})^2 + \frac{1}{2}\mu^2\phi_x^2 + \frac{\lambda}{4}\phi_x^4\right] \end{aligned} $$
and defines the (normalized) Boltzmann target, $$ \begin{aligned} p(\phi) = \frac{1}{Z}e^{-S(\phi)} \end{aligned} $$ and associated partition function (normalization constant), $$ \begin{aligned} Z = \int_{\mathbb{R}^V} e^{-S(\phi)}d\phi. \end{aligned} $$ A measure of the magnetization, the average field value over the lattice volume \(V\), can be used as an order parameter to characterize the phase transition behavior of the field: $$ \langle \phi\rangle = \tfrac{1}{V}\sum_{x\in\Lambda}\phi_x. $$
With parameters set to \( (\mu = -4, \lambda = 1) \), we obtain a theory with a broken phase realized at inverse temperature \(\beta = 1\). We show that particle methods can sample from this target in a fraction of the time required by neural methods.

Takeaways
- GPU-Accelerated JAX/blackJAX — Stochastic samplers on NVIDIA GPUs achieve very high throughput for LFT problems
- Flow-Based Sampler Trade-offs — Flow-based samplers amortize cost into training but require careful engineering of symmetries
- Strong Off-the-Shelf Baseline — Particle MC provides a robust black-box sampling alternative
- Limited Advantage Without Symmetry Knowledge — When a priori symmetry knowledge is weak, neural method advantages diminish
- Hybrid Potential — Combining stochastic samplers with learned proposals offers the best of both worlds
