Workhorse in HEP on this set of problems is Importance Sampling
- Replace problem of sampling from unknown with a known
- Adjust importance of sample drawn from by weighting,
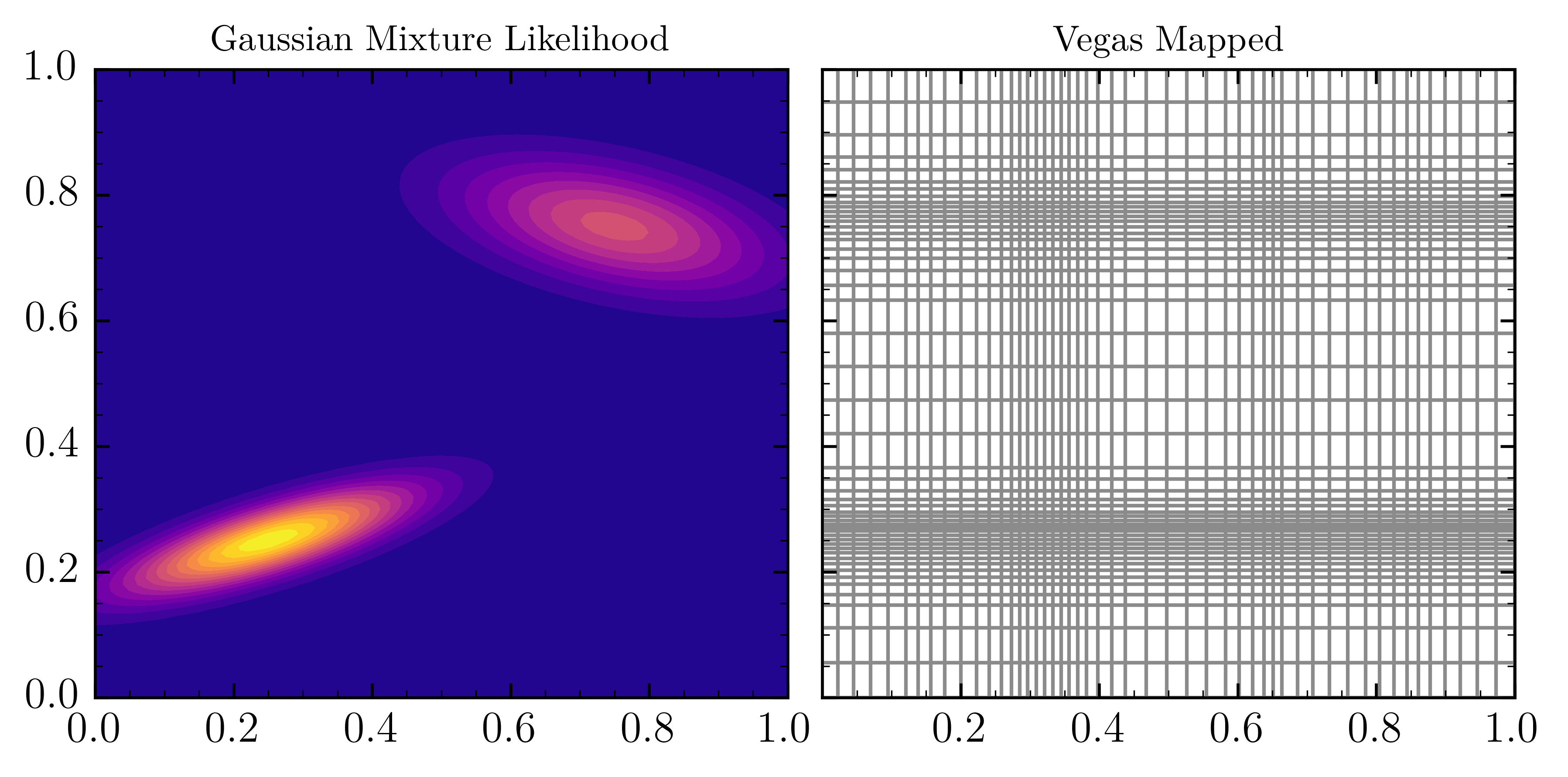
Problem seemingly reduces to coming up with good mappings for target
However, Even in Dimensions this starts to break.
- Massless glue scattering, :
- ,
- ,
Even modern ML (normalising flows) won't save you [2001.05478]
| Algorithm | Efficiency | Efficiency |
|---|---|---|
| HAAG | 3.0% | 2.7% |
| Vegas | 27.7% | 31.8% |
| Neural Network | 64.3% | 33.6% |
A sampling problem? Anyone for MCMC?
Central problem:
- Convergent integral means you have good posterior samples
- Reverse not true, Samples from a convergent MCMC chain not guaranteed a good integral
- Multimodal targets well established failure mode.
- Multichannel decompositions in MCMC HEP, (MC) [1404.4328]
MCMC kicks in as we go to high dimensions, grey area between IS and MCMC, can ML help?
Where's the Evidence?
In neglecting the Evidence () we have neglected precisely the quantity we want,
- Mapping Prior
- Matrix element Likelihood
- Cross section Evidence
Nested Sampling
Nested Sampling [Skilling 2006], implemented for in PolyChord [1506.00171]. Is a good way to generically approach this problem for dimensions
-
Primarily an integral algorithm (largely unique vs other MCMC approaches)
-
Designed for multimodal problems from inception
-
Requires construction that can sample under hard likelihood constraint
-
Largely self tuning
- Little interal hyperparameterization
- More importantly, tunes any reasonable prior to posterior
[yallup.github.io/bayeshep_durham] for animated versions
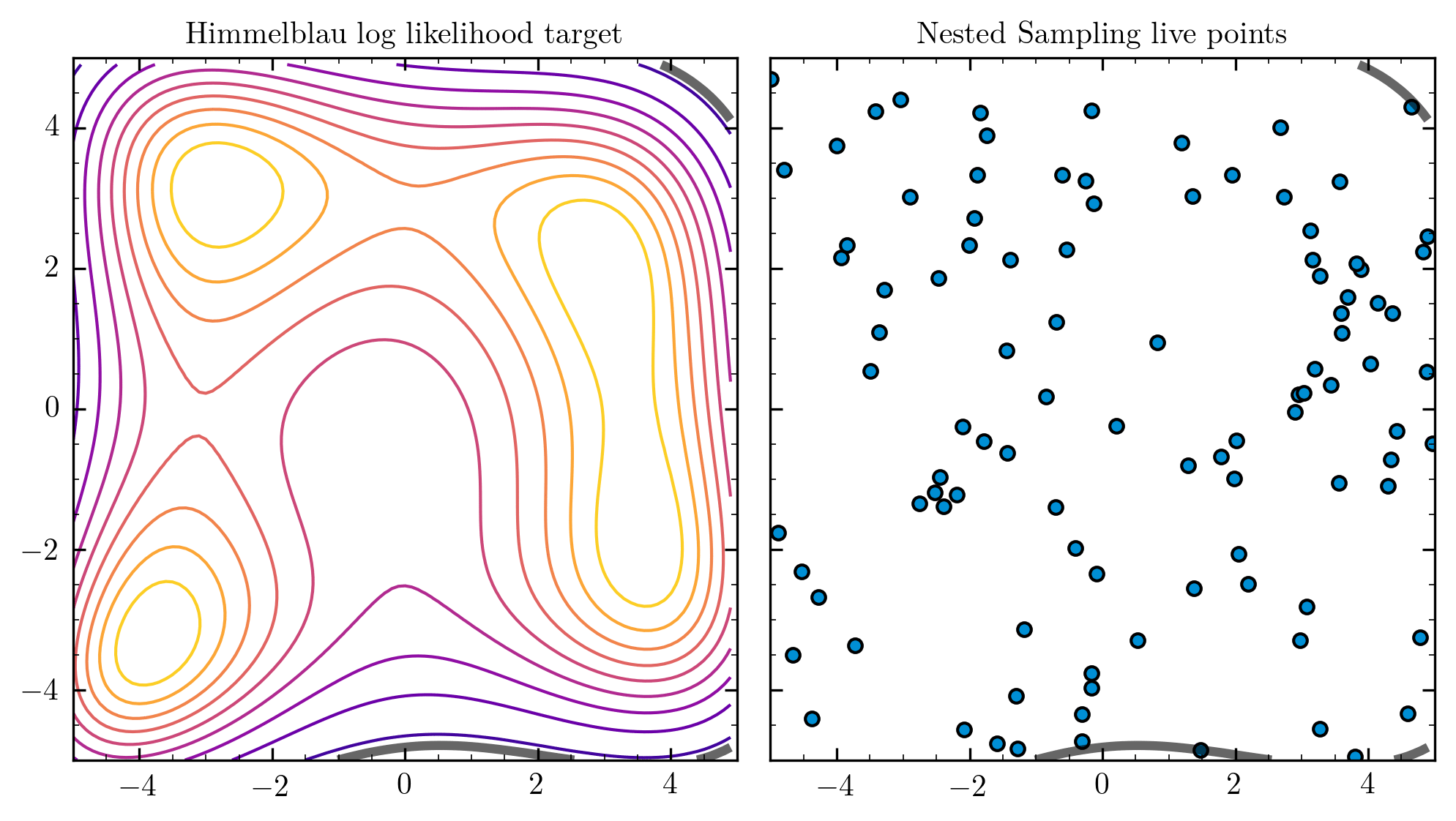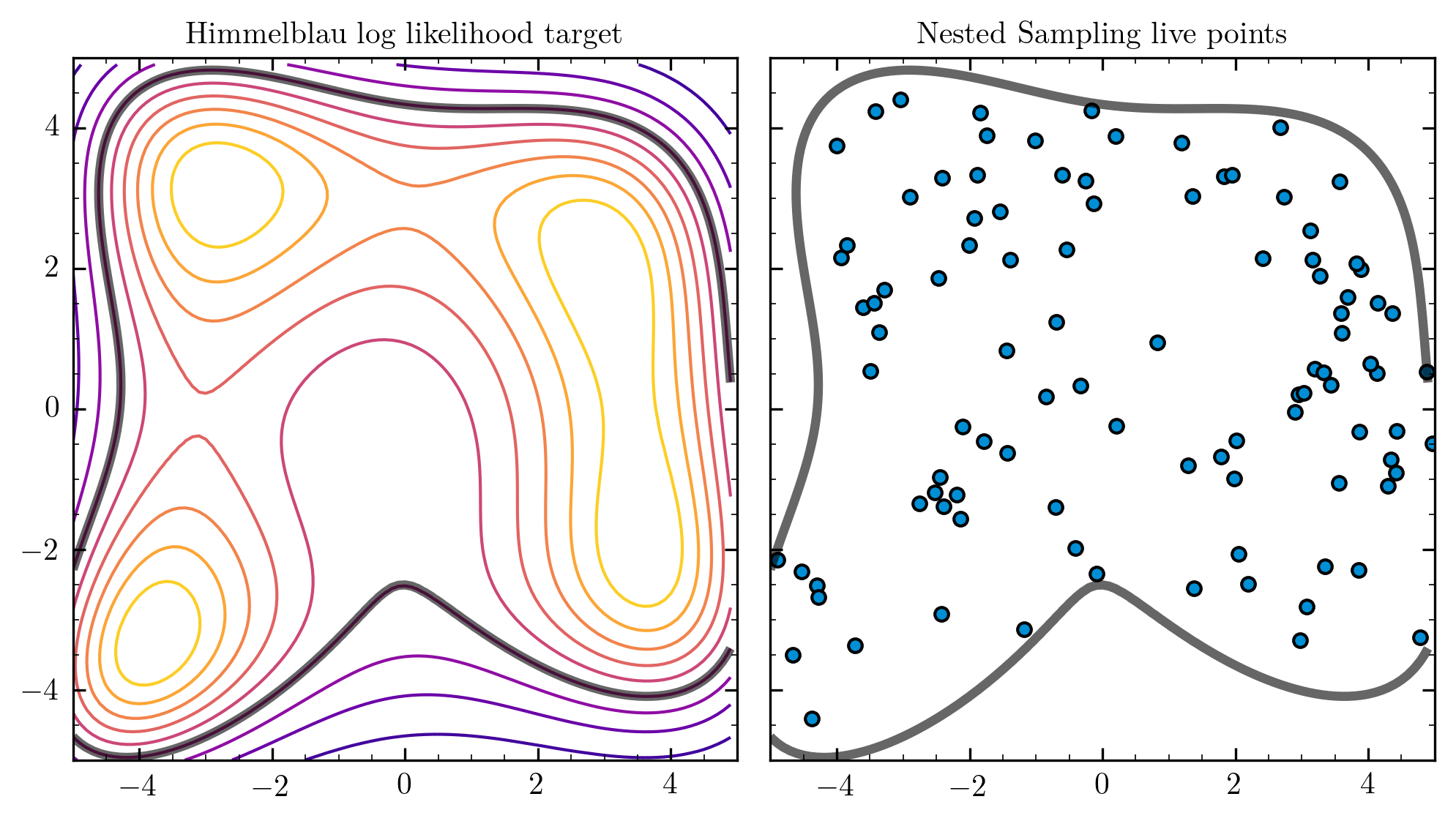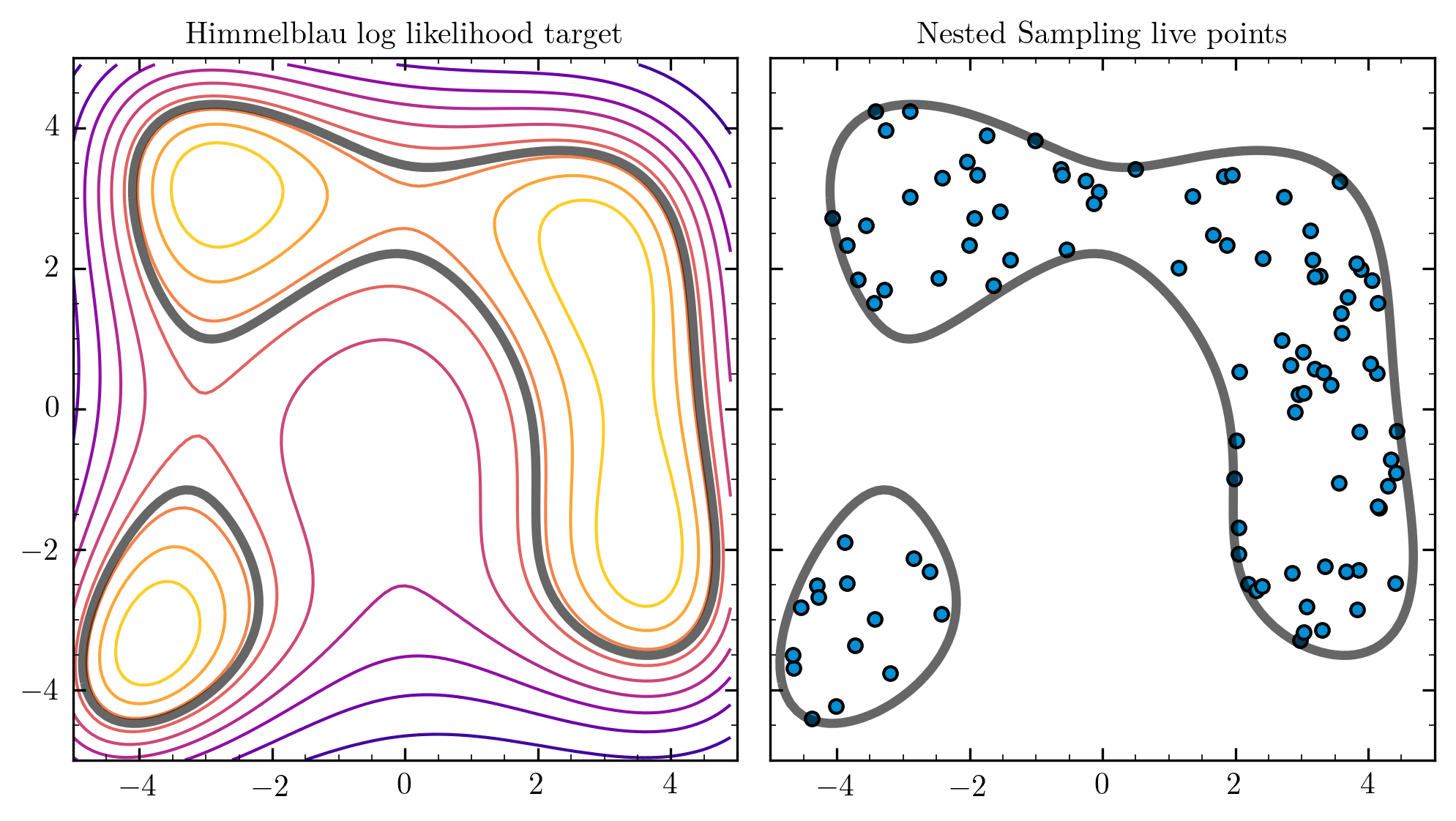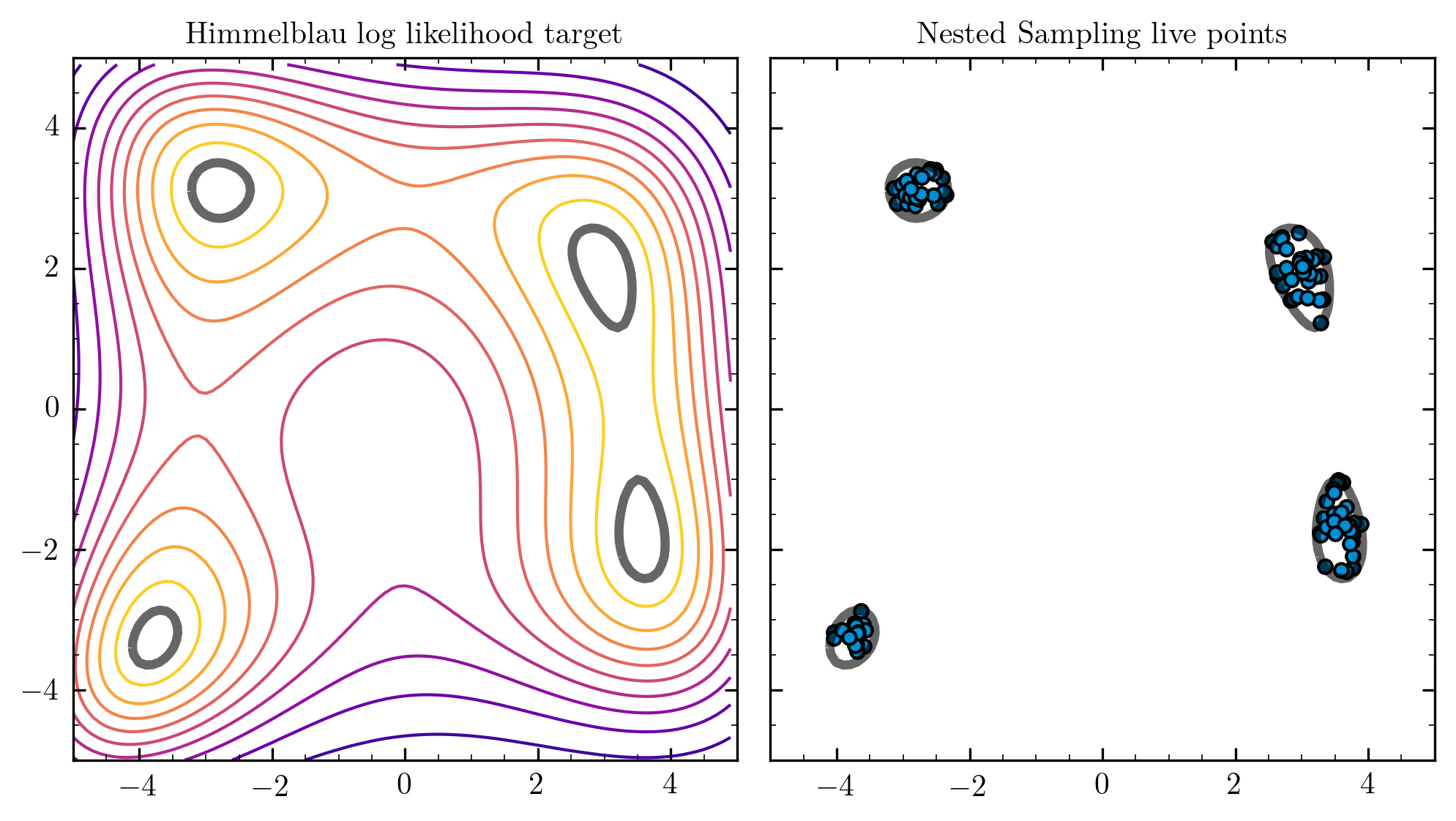
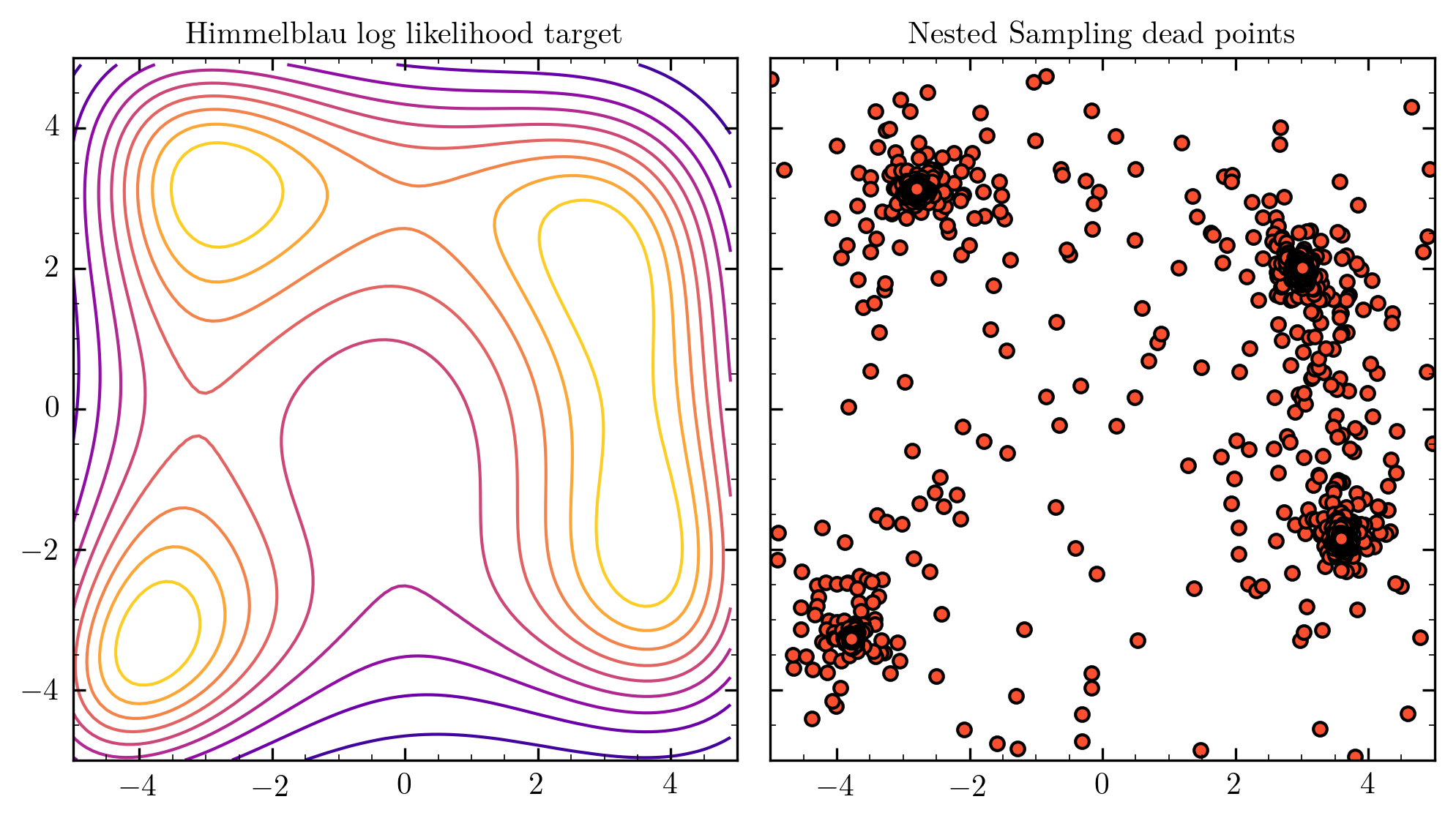
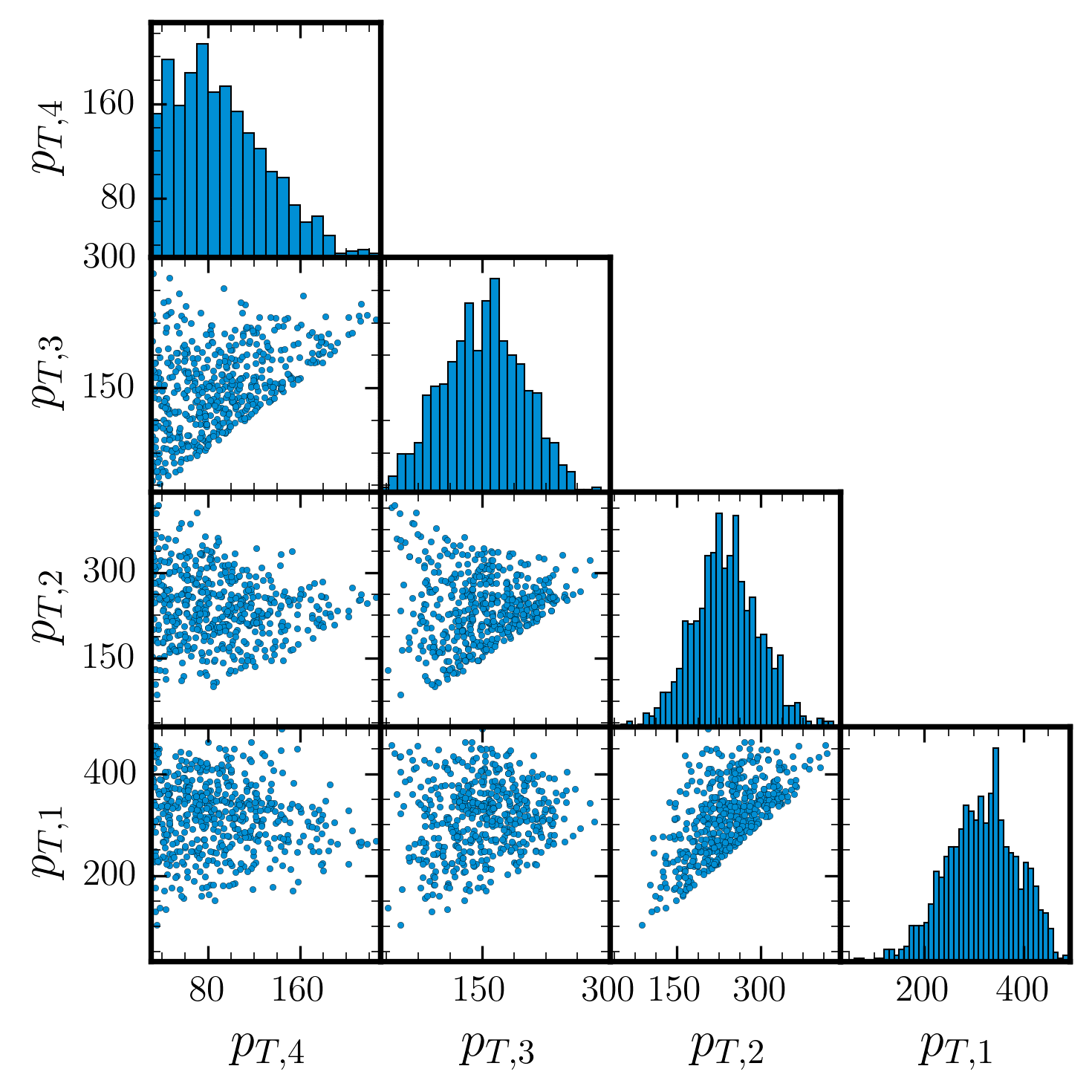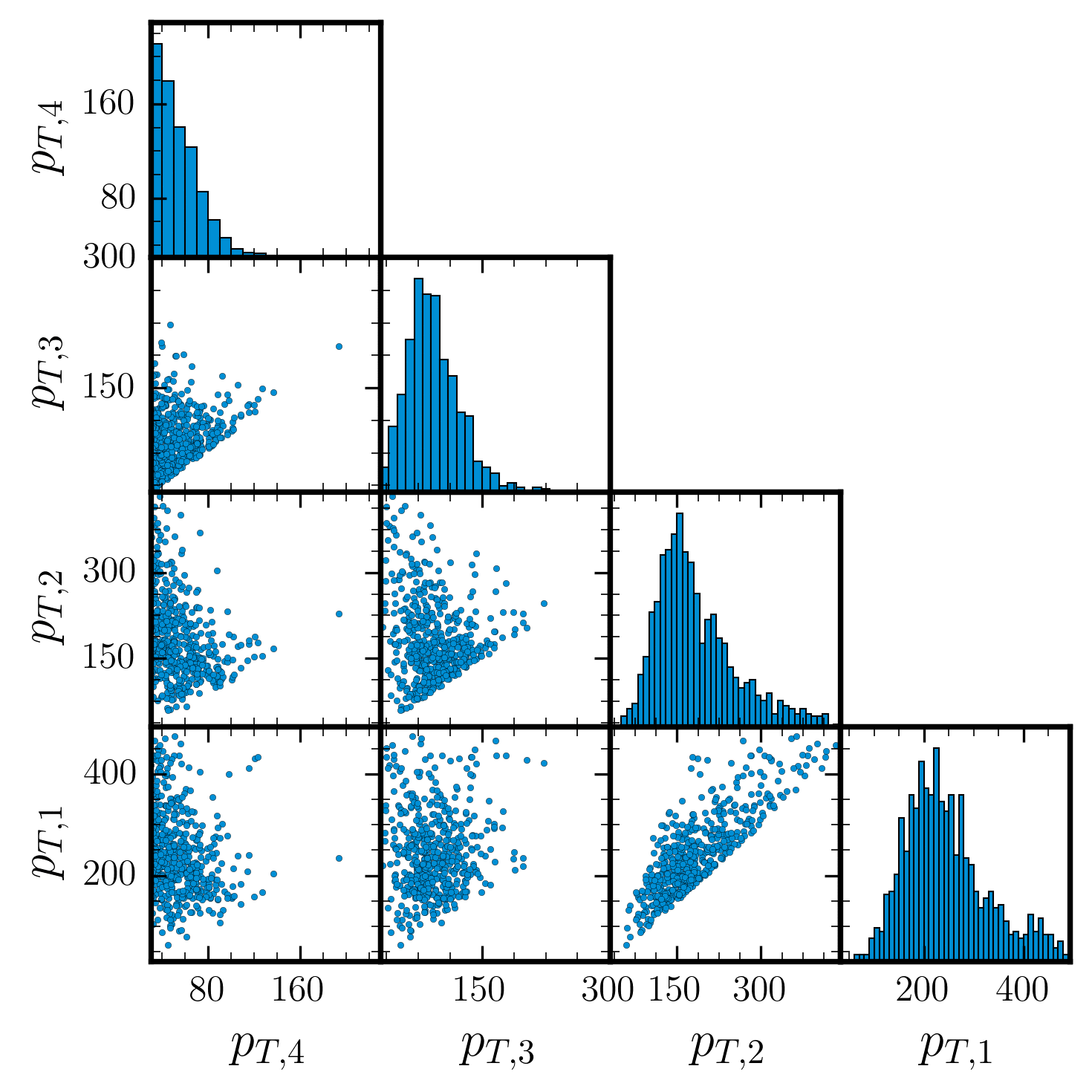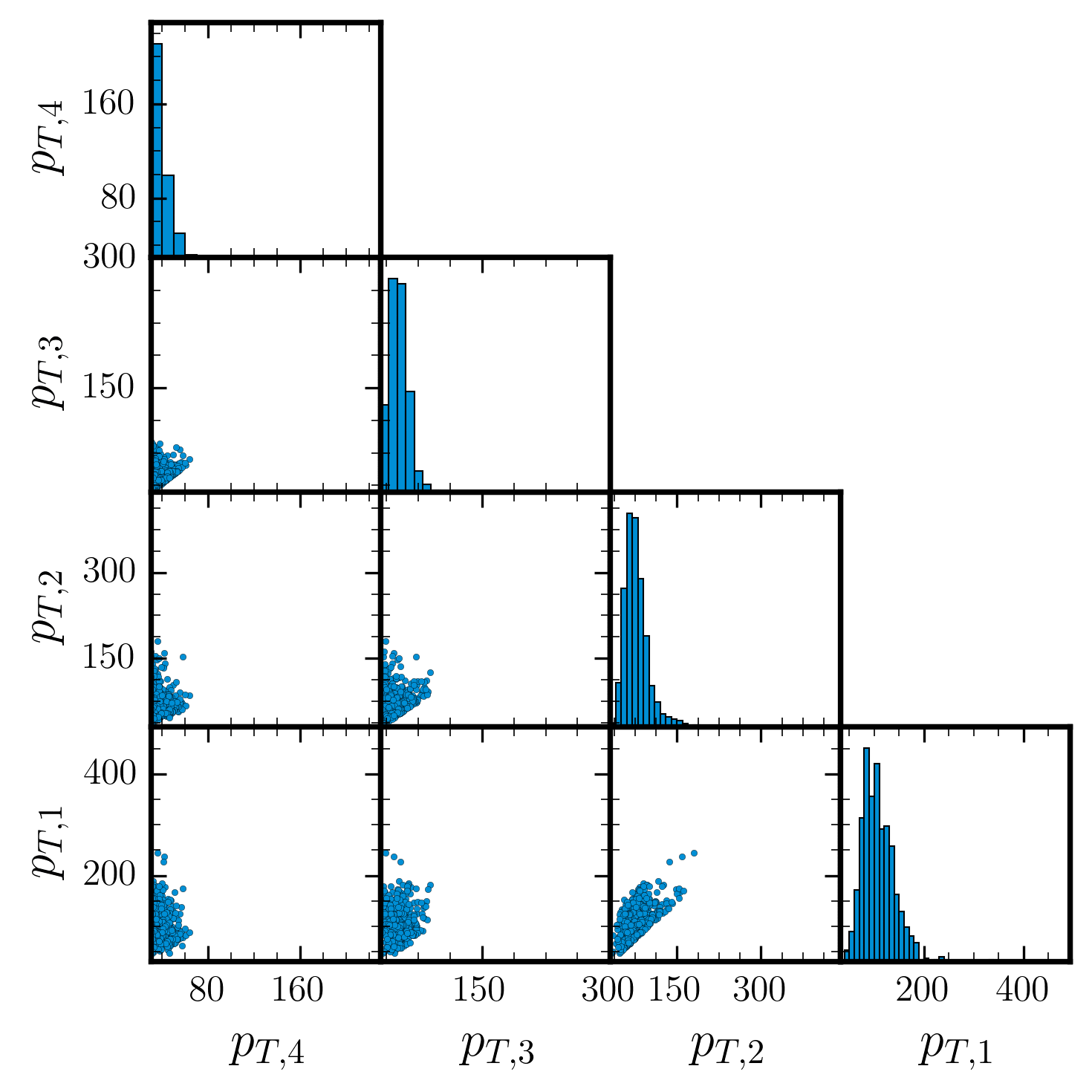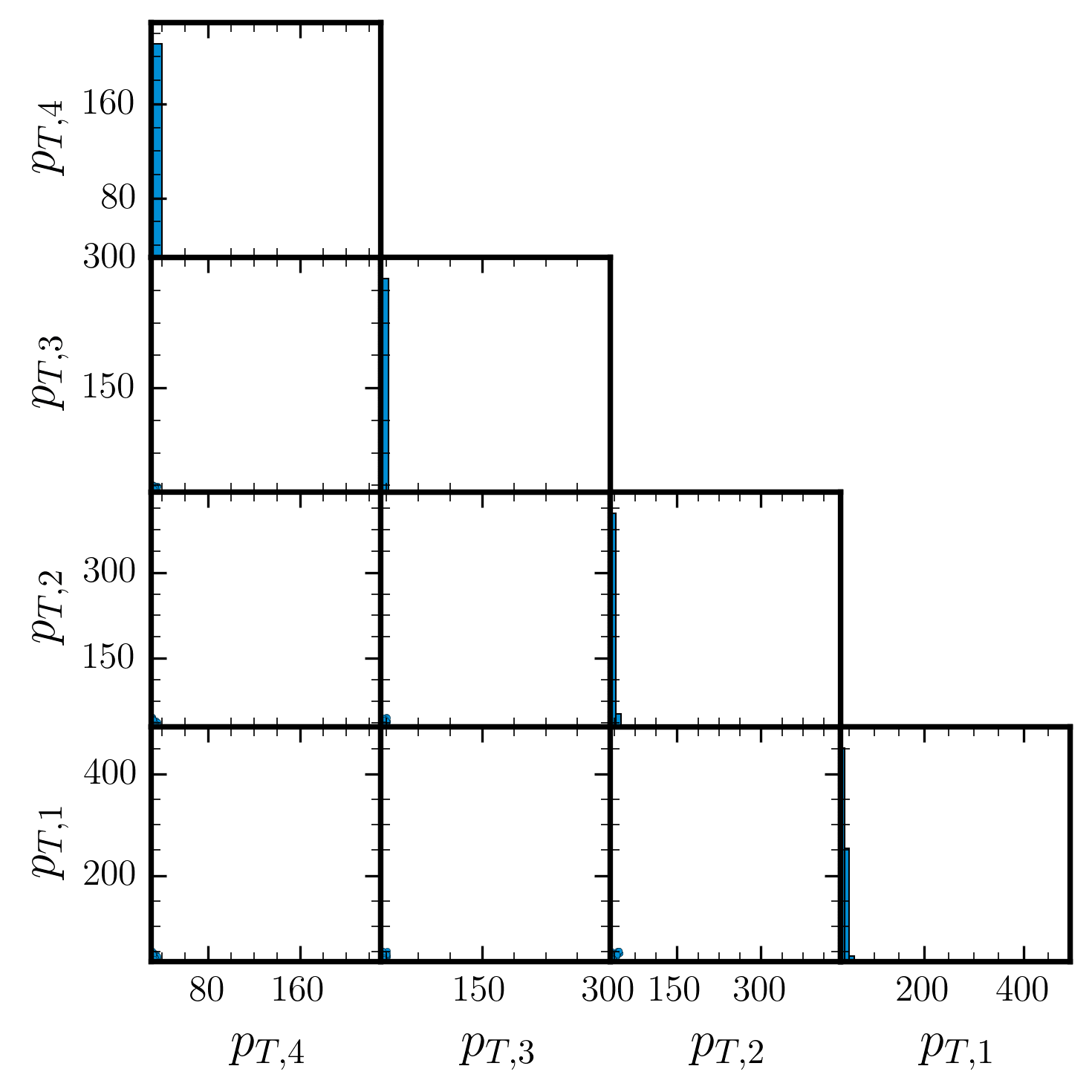
Unweighted Events
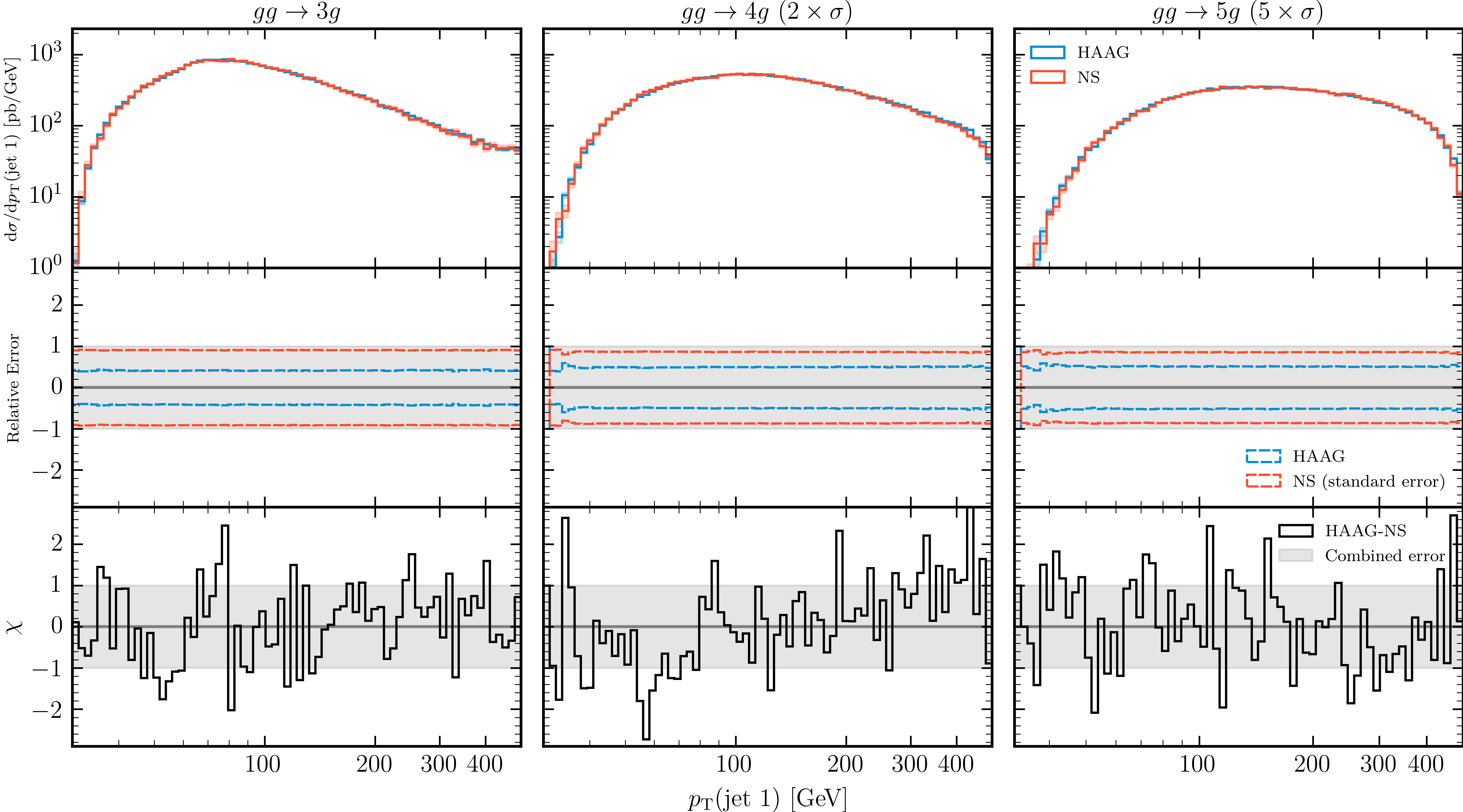
| Algorithm | |||
|---|---|---|---|
| HAAG | 3.0% | 2.7% | 2.8% |
| Vegas (cold start) | 2.0% | 0.05% | 0.01% |
| NS | 1.0% | 1.0% | 1.0% |
Where do we go from here?
End to end stylised version of the problem demonstrated.
This is deeper than coming up with a new way of mapping phase space

Where do we go from here?
(dedicated section in paper)
-
Physics challenges
-
Variants of NS algorithm
-
Prior information
-
Fitting this together with modern ML
Physics challenges
The fundamental motivation for this work came from recognising not just an ML challenge but a physics challenge [2004.13687]
LO dijet isn't hard, NNNLO is. If your method isn't robust in these limits it doesn't solve the right problem. Unique features of NS open up interesting physics:
- No mapping required: NLO proposals generically harder, NNLO more so
- No channel decomposition: can we be really clever when it comes to counter events, negative events etc. with this?
- Computation scaling guaranteed to polynomial with , other methods exponential: We can do genuinely high dimensional problems, anyone?
Conclusion
In my opinion (your milage may vary)
-
The fundamental problem for LHC event generation trying to do Importance Sampling in high dimension.
-
Machine learning can and will be useful, but this is not just a machine learning mapping problem.
-
This is a Bayesian inference problem, precisely calculating Evidences or Posterior sampling.
-
Nested Sampling is a high dimensional integration method, primarily from Bayesian Inference, that is an excellent choice for particle physics integrals